
School of Athens, Pythagoras (?)
 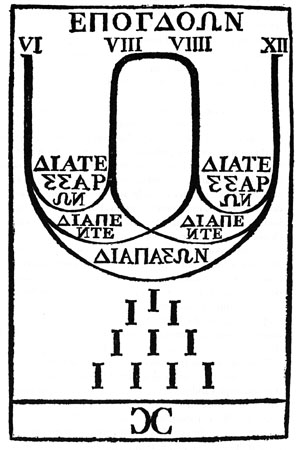
The Pythagorean Harmonic Scale, tone, diatessaron, diapente, diapason
Take four pieces of string 6", 8", 9", 12", of equal consistency, and vibrate them under equal tension
- interval between VI (6) and XII (12) = octave
- interval between VI (6), IX (9), and between VIII (8) and XII (12) = fifth
- interval between VI (6) and VIII (8), and between IX (9) and XII (12) = fourth
- interval between VIII (8) and IX (9) = major tone
Under Raphael's musical diagram is a representation a triangular figure composed of 4 rows of 10 points: I, II, III, IIII, called the tetractys, which is the Pythagorean perfect number 10. The sum of the first four figures constitutes all musical harmonies. Moreover, the Pythagorean number 10 comprises all numbers, and thus was regarded as sacred and as the "mother of the universe."
As can be seen from the tablet, 10 is the sum of the first four figures (1, 2, 3, 4) which constitutes all musical harmonies and can be associated with the philosophical concept of the Harmony of the Spheres.
The Harmonic Scale 
The Harmonic Scale, from Franchino Gaffurio. Theorica Musice (Naples, 1480), title-page. Woodcut
 Pythagoras Pythagoras
 Franchino Gaffurio Franchino Gaffurio
Harmony & Beauty: Number & Measure (Measurement & Calculation)
A common assertion in traditional creation myths is that the Maker of the World first laid down a pattern of number, from which all else proceeded. Number was thus regarded as the first archetype or paradigm of nature.
Ancient philosophers were concerned to seek out the patterns in number which correspond to those in nature, and to set them up as models in the conduct of human affairs.
Studies of a numerical character were held to be the most important in the ancient world, for they were seen to be closest to the essence of things: these were comprised of four principal disciplines:
- arithmetic
- music
- astronomy
- geometry
These constituted the major intellectual disciplines of classical education - called the Quadrivium in the Middle Ages and Renaissance, and comprised the first four of the seven Liberal Arts
The other three Liberal Arts (the Trivium) are:
- Grammar
- Rhetoric
- Dialectic
You might think of the Quadrivium in another way:
- Geometry ('Geometry' means 'measure of the earth.') and Arithmetic (measurement and calculation of forms and structures) may be understood as the study of space or spatial order.
- Astronomy, in contrast, which is the observation of the cyclic movement of the heavens, is the science of time or temporal order.
- Music provided access to harmony. The laws of simple harmonics were considered to be universals which defined the relationship and interchange between the temporal movements and events of the heavens and the spatial order and development on earth. So music was the connecting link between time and space, and between man and the cosmos, and the destiny of both.
Geometry, arithmetic, astronomy, music are all number-based disciplines. The study and manipulation of number was very ancient.
According to Plato in Laws, the Egyptian priests, who controlled education, ensured that all who sought advancement in life studied and worked according to the sacred canon of number and proportion. This, said Plato, had the effect of maintaining the level of culture for at least ten thousand years. It was the chief objective of Pythagoras and his school to reconstitute and reinvigorate the ancient numerical code and the philosophy associated with it.
The respect and veneration formerly given to numerical studies arose from the understanding that not only could the intervals of music, the ratios of geometry, astronomical periods, and the cycles of time be measured by the same standards of number, but that the numerical patterns to which they conformed were also somehow inherent in the structure of the human mind. Plato believed that human nature, like the nature of the entire universe, was essentially number-based.
In the ancient world, it was long recognized that the power of music lay in the fact that the human mind was numerically structured. The intervals in music clearly express numerical ratios (as shown by Pythagoras), and of all the arts, music has the most direct effect on human emotions. This allows it to be used, for better or worse, to manipulate individuals and masses.
The earliest legendary rulers, the Orphic bards, were said to legislate through music alone, and the priests of later times were most careful in upholding the traditional musical scales because these, by resonance, were inclined to invoke corresponding harmonies in the human soul. Innovations in musical form were by the same token forbidden because of their disruptive tendencies. As Plato observed, changes in government are brought about by changes in music.
In the Renaissance
Recognition of the mathematical and harmonic structure of the universe and all creation
"...new scientific approach to nature among 15th century Italian artists. It was the artists, headed by Alberti, who had a notable share in consolidating and popularizing the mathematical interpretation of all matter. They found and elaborated correlations between the visible and intelligible world... Architecture was regarded by them as a mathematical science which worked in spatial units: parts of that universal space for the scientific interpretation of which they had been discovered the key in the laws of perspective. Thus they were made to believe that they could re-create the universally valid ratios and expose them pure and absolute, as close to abstract geometry as possible. And they were convinced that universal harmony could not reveal itself entirely unless it were realized in space through architecture conceived in the service of religion." [Rudolf Wittkower, Architectural Principles in the Age of Humanism, 1949, p. 29]
|

